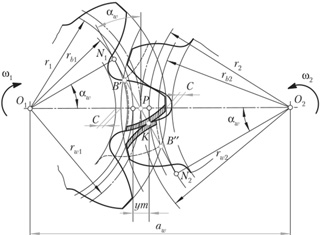
Геометрические параметры циклоидальной передачи

В ремонт же поступают ЦП с разницей чисел зубьев больше одного и выходным элементом, связанным с большей шестерней (внутреннего зацепления). Например, редуктор вспомогательного привода шаровой мельницы.

Рис. 1. Первая ступень циклоидного редуктора в разобранном состоянии

Общее передаточное число 886, двухступенчатый, модуль первой ступени — 2,5 мм, модуль второй — 3,5 мм, число зубьев шестерен первой ступени 168 и 162, второй соответственно 190 и 184, эксцентриситет первой ступени 7,5 мм, второй — 10,5 мм, высота зуба первой ступени 5 мм, второй — 7 мм. Соотношение высоты зуба и модуля отличается от эвольвентного.

Рис. 2. Первая ступень циклоидного редуктора в собранном состоянии. Вид со стороны циклоидных шестерен

Для квалифицированного освоения ЦП требуется разработка теоретической базы. Для специалистов, знакомых с устройством планетарных передач (ПП), удобно начать знакомство с циклоидальными передачами по аналогии с планетарными, тем более что некоторые авторы считают ЦП разновидностью планетарных [3, стр. 217]. Планетарными передачами называют зубчато-рычажный механизм, в котором некоторые элементы совершают сложное движение, состоящее из переносного (вместе с водилом) и относительного (относительно водила) вращательных движений [4]. В этом смысле циклоидальные передачи подпадают под это определение. Общие для ЦП и ПП элементы — эпициклические шестерни внутреннего зацепления.

Рис. 3. Эпицикл первой ступени циклоидного редуктора, являющийся входным элементом второй ступени

Различия ЦП и ПП в шестернях внешнего зацепления: в ПП их две — солнце и сателлит. Солнце — это центральное зубчатое колесо, вращающееся относительно основной оси ПП. Сателлит (или группа сателлитов) — вспомогательное зубчатое колесо, установленное на подшипниках на оси, закрепленной на водиле. В ЦП шестерня внешнего зацепления одна (может быть несколько одинаковых, как групп сателлитов в ПП).Она подобна сателлиту в том, что: 1) циклоидальная шестерня ЦП совершает сложное движение: переносное вместе с эксцентриком и относительное относительно эксцентрика; 2) находится в зацеплении с эпициклом ЦП. Роль солнечной шестерни ПП в ЦП выполняет эксцентрик.

В процессе изучения ЦП установлено следующее: 1) , где ∆z — разница чисел зубьев на коронной и внутренней шестернях ЦП, e — эксцентриситет ЦП (мм), m — модуль, мм;

2) Передаточное число редуктора: а) для ЦП, в которой выходной вал соединен с эпициклом, i = , где z_Б — число зубьев на эпицикле (на большей шестерне); б) для ЦП, в которой выход — это водило i = , где z_м — число зубьев на малой, внутренней шестерне внешнего зацепления.

В ЦП с выходом от водила [1], контакт циклоидальной шестерни с водилом, осуществляется перекатыванием отверстия в шестерне по цевке. Первоначально, при анализе редуктора вспомогательного привода шаровой мельницы было предположено, что опора на корпус осуществляется аналогично — через контакт отверстия в циклоидальной шестерне с цевкой. Но впоследствии это предположение было отвергнуто, хотя оно видимо тоже возможно.

Рис. 4. Первая ступень циклоидного редуктора в собранном состоянии. Вид со стороны входного вала

При рассмотрении конструкции (см. рис. 1–4) установлено, что имеется две циклоидальных шестерни, работающие в противофазе. Каждая имеет подшипниковую опору не только на входном эксцентричном валу, но еще по 4 подшипниковых опоры, установленные в корпусе на эксцентриках. Что в итоге обеспечивает движение каждой точке циклоидной шестерни по окружности радиусом, равным эксцентрику.

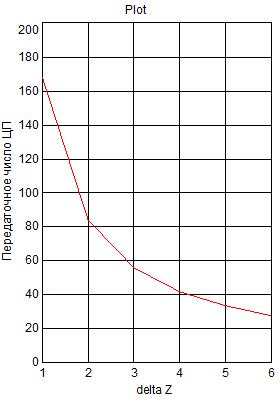
Рис. 5. Передаточное число ЦП
в зависимости от разницы
ΔZ чисел зубьев на эпицикле
и циклоидной шестерне (при Z_э=168)

На фото рис. 4 видно: 

1) все пять эксцентриков установлены согласованно (см. риски на осях эксцентриков и расположение эксцентрика в центре) и могут работать только синхронно. Таким образом, одна шестерня не может произвольно проворачиваться относительно другой на своем центральном подшипнике;

2) то, что в «классической» схеме ЦП является цевкой здесь всего лишь деталь, соединяющая две корпусные детали, внутри которых смонтированы две циклоидальные шестерни; 

3) отверстия в шестернях сделаны для свободы расположения этих цевок, диаметр отверстий должен гарантировать зазор между неподвижными цевками и совершающими сложное движение шестернями.

4) Крутящий момент подается от приводного электродвигателя на центральный вал через шпонку, опора на корпус осуществляется через четыре подшипниковых опоры на периферии

Применение редуктора с выходом от эпицикла вместо редуктора с выходом от водила увеличивает передаточное число каждой ступени всего на 1, а в итоге передаточное число редуктора в целом увеличивается с 840 до 886.

Передаточное число ЦП зависит от числа зубьев на эпицикле и разницы чисел зубьев на эпицикле и циклоидной шестерне, как показано на рис. 5. Для подбора заданного передаточного числа необходимо после назначения возможной разницы ΔZ подобрать Z_э.

По кинематическим и силовым соотношениям данная ЦП эквивалентна планетарному механизму со спаренными сателлитами, эпициклом и солнцем [4]. Силовые соотношения имеют вид: М_э=М_с*к; М_в=М_с*(к-1); где к=Z_э/ΔZ; М_э — момент на эпицикле; М_с — момент на эксцентрике; М_в — момент на водиле.

Коэффициент полезного действия циклоидальной передачи. В источнике [2] утверждается, что КПД циклоидального редуктора составляет 95% в одной ступени и 90% — в двух ступенях. Необходимо удостовериться в большом КПД ЦП. Если рассматривать ЦП как разновидность ПП, то КПД определяется количеством зубчатых зацеплений. Согласно [4] внутренний КПД передачи с одним внутренним зацеплением равен 0,99. Надо уточнить, что здесь учтены потери только в зубчатом зацеплении, в предположении, что все остальные потери на порядок меньше. Вопрос требует уточнения. В [3] приведена формула для расчета КПД зубчатой передачи с учетом основных всех потерь:

η = 1 - (ψ_з + ψ_м + ψ_п)

где ψ_з — потери на трение в зацеплении, ψ_м — потери на перемешивание масла, ψ_п — потери на трение в подшипниках.

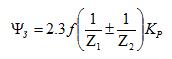
Согласно [3] примем f=0.08, K_p=1.4, в скобках знак «плюс» для внешнего зацепления, «минус» — для внутреннего зацепления. Определим ψ_з для Z₁=162 и Z₂=168:

Удостоверимся, что для обычного, среднестатистического внутреннего зацепления, с гораздо меньшим числом зубьев на внутренней (малой) шестерне эти же потери соразмерны с 1%, как и утверждается в [4].

, то есть 0.6%.

А для внешнего зацепления — близки к 2%:

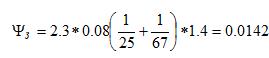, то есть 1.4%

Чем меньше зубьев на меньшей шестерне — тем больше потери.

Разумно утверждать, что потери в подшипниках и на перемешивание масла одинаковы для вальных, планетарных и циклоидальных передач.

Таким образом, циклоидальная передача имеет преимущество по КПД перед всеми вальными и планетарными передачами, по причине большого количества зубьев на малой шестерне.

О крутящем моменте, передаваемом исследованным циклоидальным редуктором. Редуктор приводится во вращение электродвигателем номинальной мощностью 7,5 кВт при частоте вращения 900 об/мин, таким образом, крутящий момент на входе в редуктор — 80 Нм. На выходе ω=1 об/мин, а М_кр= 80*900=72000 Нм.

Для сравнения потребный крутящий момент на выходе бортового редуктора трактора ТМ-10 производства ООО «ДСТ Урал» можно оценить по силе тяги на ведущих колесах по 10 т на каждом борту и радиусу ведущего колеса:

Мвк = 100000H * 0,43м = 43000 Нм

Таким образом, и по крутящему моменту ЦП может быть применена в качестве бортового редуктора промышленного трактора. 

Выводы:

1. Изучена схема циклоидальной передачи с выходом от эпицикла;
2. Такая схема по силовым и кинематическим соотношениям эквивалентна планетарному механизму со спаренными сателлитами, эпициклом и солнцем;
3. Установлены зависимости между числом зубьев на шестернях, передаточным числом циклоидальной передачи и эксцентриситетом;
4. Показано преимущество циклоидальной передачи по КПД перед вальными и планетарными передачами;
5. Выработаны рекомендации по проектированию циклоидальной передачи с заданным передаточным числом;
6. Рассмотрена возможность применения циклоидальной передачи в качестве бортового редуктора промышленного трактора класса 15-20.

Литература:

1. Википедия. Циклоидальная передача. https://ru.wikipedia.org/wiki
2. Интернет ресурс. http://www.darali.com/page17.html
3. Решетов Д. Н. Детали машин: Учебник для студентов машиностроительных и механических специальностей вузов. — 4-е изд., перераб. и доп. — М.: Машиностроение, 1989.- 496 с.
4. Филичкин Н. В. Анализ планетарных коробок передач транспортных и тяговых машин: Учебное пособие. — Челябинск: Изд. ЮУрГУ, 2005. — 175 с.